6th grade Q4

How do you determine the relationship of the volume between a cylinder and sphere?

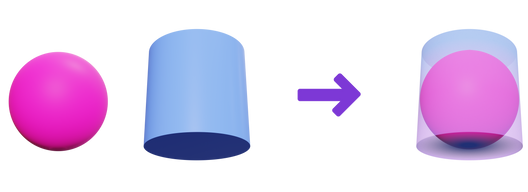
The volume of a sphere is exactly two third the volume of a cylinder if the cylinder and the sphere have the same base radius and the height of the cylinder is equal to the diameter of the sphere.

This is the reason why:

Volume of the Sphere:
You use the formula for the volume of a sphere:

This formula is standard and it calculates the volume based on the radius $r$ of the sphere.

V_{s p h ere} = \frac{4}{3} π r^{3}

Volume of the Cylinder:
Given that the height of the cylinder $h$ equals the diameter of the sphere, which is $2 r$ , you substitute this value into the formula for the volume of a cylinder:

Substitute $h = 2 r$ into this formula:

So, the volume of the cylinder becomes $2 π r^{3}$ .

V_{cy l in d er} = π r^{2} h

V_{cy l in d er} = π r^{2} (2 r) = 2 π r^{3}

Finding the Ratio of Volumes:
You want to find out how many times the volume of the sphere is of the volume of the cylinder. For that, you set up a ratio:

Plug in the volumes we calculated:

Ratio = \frac{V _{co n e}}{V _{cy l in d er}}

Ratio = \frac{\frac{4}{3} π r ^{3}}{2 π r ^{3}}

Simplifying the Ratio:
In this fraction, $π r^{3}$ appears in both the numerator and the denominator, so it can be cancelled out:

Simplify this fraction:

Ratio = \frac{\frac{4}{3}}{2}

Ratio = \frac{4}{3} \times \frac{1}{2} = \frac{4}{6} = \frac{2}{3}

So, the volume of the sphere is $\frac{2}{3}$ of the volume of the cylinder under these conditions:

V_{s p h ere} = \frac{2}{3} V_{cy l in d er}

This ratio means that if you had a cylinder and a sphere with the given dimensions, the sphere's volume would fill two-thirds of the cylinder's volume.

Example:

If a cylinder has the volume of 30 cubic units, the sphere with the same base and height has the volume of 20 cubic units.